研究発表
- 複合大域シミュレーション
- 研究発表
ランダウ減衰・シュレディンガー方程式・ゆらぎの定理
核融合科学研究所複合大域シミュレーションユニットの洲鎌英雄教授が、「ランダウ減衰・シュレディンガー方程式・ゆらぎの定理」についての研究成果をまとめ、その論文が「Physics of Plasmas」の2025年8月号に掲載されました。
【論文概要】
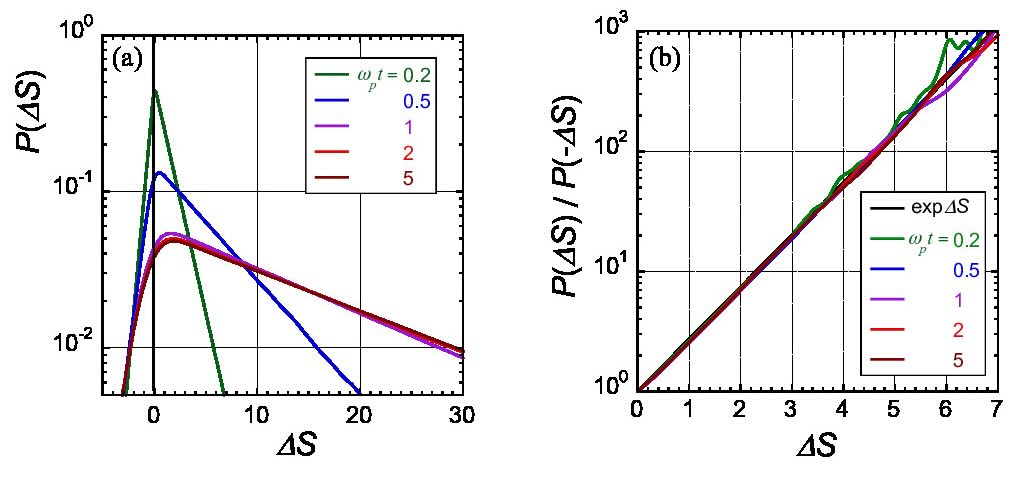
ランダウ減衰は、宇宙空間や核融合装置などの高温プラズマにおいて見られる波動加熱のほか、微視的不安定性やゾーナルフローの振動現象 (GAM) 等を安定化させる主要な物理機構の一つとして、これまで広く研究されてきた。ランダウ減衰は、時間反転対称性をもつブラゾフ方程式に従う無衝突プラズマで起こる現象であるにもかかわらず、一見すると非可逆的な過程に思われる。一方、可逆的な力学から導かれるゆらぎの定理は、エントロピーの生成と減少の確率の比が時間とともに指数関数的に増大することを示し、それによって熱力学第二法則および非平衡統計力学を基礎づけすることができる。本論文は、線形ブラゾフ-ポアソン方程式系を、時間反転対称性や保存則を簡潔に表すため、シュレディンガー方程式の形に定式化した。この定式化によって、粒子速度分布関数の確率密度汎関数から定義される確率的相対エントロピーに関してゆらぎの定理が成立することが示された。平衡温度で規格化されたエネルギー変動分とエントロピー変動分との差は、系の時間に依存しない不変量となるが、この不変量は、速度分布関数の摂動成分の2次形式となり、シュレディンガー方程式を満たす状態ベクトルの2乗振幅に対応する。また、ケース-ファン・カンペンモードに対応するハミルトニアンの固有ベクトルが導出された。このハミルトニアンの固有ベクトルから厳密解を構成し、それを用いることよって、ランダウ減衰過程に対するゆらぎの定理が定式化され、その妥当性が数値シミュレーションによって検証された。これらの結果は、非平衡統計力学の観点からの無衝突プラズマ物理過程の新たな定式化に貢献するものである。
【論文情報】
