研究発表
- 複合大域シミュレーション
- 研究発表
一次元ブラゾフ-ポアソン系における情報エントロピーの時間発展
核融合科学研究所の連携大学院生で複合大域シミュレーションユニットのメンバーである東京大学大学院新領域創成科学研究科先端エネルギー工学専攻博士課程3年生の前角弘毅らが「Time evolutions of information entropies in a one-dimensional Vlasov–Poisson system」についての研究成果をまとめ、その論文が「Physics of Plasmas」の2024年10月号に掲載されました。さらに、本論文はFeatured Articleに選ばれました。
【論文概要】
1次元のブラゾフ-ポアソン系において、電子の位置と速度変数の確率分布関数の情報エントロピーがランダウ減衰過程においてどのように発展するかが示された。cos関数形の空間分布を持つ密度摂動とマクスウェル速度分布によって与えられた初期条件から、早期および長期双方の時間領域における分布関数と電場の挙動を正確に記述する線形および準線形解析解が導出され、これらの解の妥当性が、等高線力学法(Contour-Dynamics)に基づく非線形数値シミュレーションとの比較によって確認された。導かれた準線形解析解を用いることにより、速度分布関数の時間発展と、ガウス分布からのずれを示す尖度(kurtosis)が、摂動振幅の2乗の精度で求められ、電子の位置と速度変数の情報エントロピーとそれらの相互情報量の時間発展過程が明らかにされた。さらに、クーロン衝突を考慮することより、無衝突過程の最終状態から熱平衡状態への緩和過程を考察し、衝突緩和過程では、位置変数と速度変数の相互情報量が0に減少する一方で、位相空間分布関数の全情報エントロピーは相互情報量の減少分だけ増加することによって、ボルツマンの H 定理が成立することが確認された。
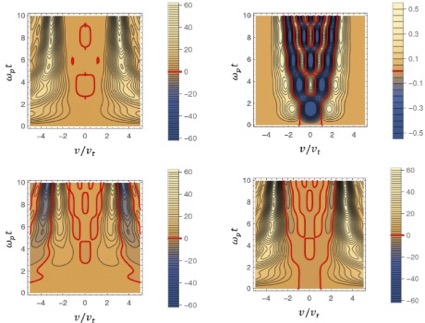
本研究は、核融合科学研究所のプラズマシミュレータ雷神を使用して行われました。
【論文情報】
DOI: 10.1063/5.0227622
