Report

  • Complex Global Simulation
  • Report

Time evolutions of information entropies in a one-dimensional Vlasov–Poisson system

Koki Maekaku et al. summarized their research as “Time evolutions of information entropies in a one-dimensional Vlasov–Poisson system,” and their paper has been published in Issue 10 of Physics of Plasmas. In addition, this paper has been selected as a Featured Article.

【Abstract】
A one-dimensional Vlasov–Poisson system is considered to elucidate how the information entropies of the probability distribution functions of the electron position and velocity variables evolve in the Landau damping process. Considering the initial condition given by the Maxwellian velocity distribution with the spatial density perturbation in the form of the cosine function of the position, we derive linear and quasilinear analytical solutions that accurately describe both early and late time behaviors of the distribution function and the electric field. The validity of these solutions is confirmed by comparison with numerical simulations based on contour dynamics. Using the quasilinear analytical solution, the time evolutions of the velocity distribution function and its kurtosis indicating deviation from the Gaussian distribution are evaluated with the accuracy of the squared perturbation amplitude. We also determine the time evolutions of the information entropies of the electron position and velocity variables and their mutual information. We further consider Coulomb collisions that relax the state in the late-time limit in the collisionless process to the thermal equilibrium state. In this collisional relaxation process, the mutual information of the position and velocity variables decreases to zero, while the total information entropy of the phase-space distribution function increases by the decrease in the mutual information and demonstrates the validity of Boltzmann’s H-theorem.

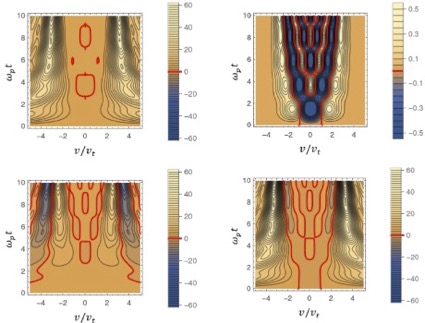
Figure: Contours of the change in the kinetic energy Δε(v,t)/(α2 T) (top-left), the information content (self-entropy) ΔS(v,t)/(α2 T) (bottom-left) obtained from of the electron velocity distirubion, the deviation of the velocity distribution function from the Maxwellian equilibrium f2 (v,t)/(α2 n0 vt-3 ) (top-right), and f2 (v,t)/(α2 f0M (v)) (bottom-right) on the (v,t) plane for kλD=1/2. The red lines indicate the contours where each quantity is zero.

The numerical simulations were performed on Plasma Simulator of NIFS.

【Publication】

K. Maekaku, H. Sugama, T.-H. Watanabe; “Time evolutions of information entropies in a one-dimensional Vlasov–Poisson system”, Phys. Plasmas 31, 102101 (2024).
DOI: 10.1063/5.0227622

↑